LeetCode #23 Merge k Sorted Lists

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

在這次問題中，嘗試使用 Go 來實作三種不同的解題方式，總結其複雜度分析如下，假設有 k sorted lists，且共有 N 資料元素 (數值)：

實作解法	空間複雜度	時間複雜度
暴力排序法	O(N)	O(NlogN)
尋找最小值	O(1)	O(Nk)
使用 Priority queue	O(k)	O(Nlogk)

分析與解法 - 暴力排序法

最直觀且直覺的想法，是列舉所有資料元素，把所有的數值塞到一個陣列中，然後執行排序演算法後，再輸出結果。

且 Go 標準函式庫已經有實作排序 sort，直接拿來使用就可以了

/**
* Definition for singly-linked list.
* type ListNode struct {
*    Val int
*    Next *ListNode
* }
*/
import(
   "sort"
)

type nodeSorter struct {
   vals []*ListNode
}

func (ns nodeSorter) Len() int {
   return len(ns.vals)
}

func (ns nodeSorter) Less(i, j int) bool {
   return ns.vals[i].Val < ns.vals[j].Val
}

func (ns *nodeSorter) Swap(i, j int) {
    t := ns.vals[i]
    ns.vals[i] = ns.vals[j]
    ns.vals[j] = t
}

func mergeKLists(lists []*ListNode) *ListNode {
   vals := make([]*ListNode, 0)
   for _, list := range lists {
      for itr := list; itr != nil; itr = itr.Next {
         vals = append(vals, itr)
      }
   }
   if len(vals) <= 0 {
      return nil
   }
   sort.Sort(&nodeSorter{vals})
   for i := 1; i < len(vals); i++ {
      vals[i-1].Next = vals[i]
   }
   vals[len(vals)-1].Next = nil
   return vals[0]
}

假設 k lists 中，共有 N 個資料元素，計算此演算法複雜度：

空間複雜度：O(N)
- 需要將所有資料塞入到陣列中排序
時間複雜度： O(NlogN)
- 列舉將所有資料元素，並塞入到陣列 O(N)
- Go 排序是採用 Quick Sort，取一般情況 O(NlogN)

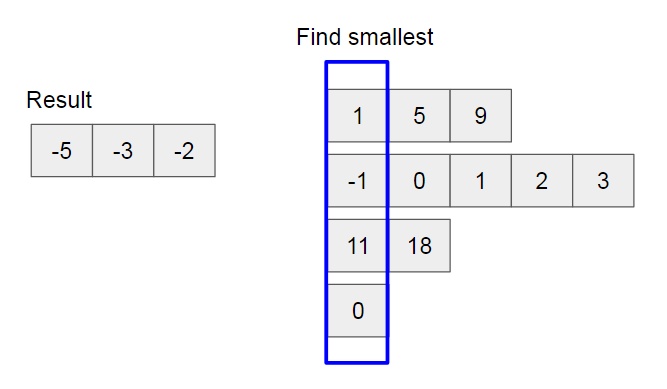
分析與解法 - 尋找最小值

考慮已知條件，k 個 lists 本身內資料元素已經有排序，因此可以考慮每次從 k lists 挑出最小的數值，直到每一個 list 都沒有元素，最後完成輸出。

演算法示意圖，每次都從 lists 中挑出最小的數值

/**
* Definition for singly-linked list.
* type ListNode struct {
*    Val int
*    Next *ListNode
* }
*/

func mergeKLists(lists []*ListNode) *ListNode {
   var head, itr *ListNode
   for true {
      // Find smallest
      sidx := -1
      for i := 0; i < len(lists); i++ {
         comparer := lists[i]
         if comparer != nil {
            if sidx < 0 || comparer.Val < lists[sidx].Val {
               sidx = i
            }
         }
      }
      if sidx < 0 {
         break
      } else {
         if itr == nil {
            head = lists[sidx]
            itr = head
         } else {
            itr.Next = lists[sidx]
            itr = itr.Next
         }
         lists[sidx] = lists[sidx].Next
      }
   }
   if itr != nil {
      itr.Next = nil
   }
   return head
}

假設 k lists 中，共有 N 個資料元素，計算此演算法複雜度：

空間複雜度：O(1)
- 不需要額外配置資料陣列 (allocate array)
時間複雜度：O(Nk)
- 列舉所有資料元素 O(N)
- 每次從 k lists 中挑出最小的資料 O(k)

分析與解法 - 使用 Priority queue

這算是上一個演算法的改良吧，自己並沒有在第一時間想到，而是完成以上兩種演算法實作後，搜尋別人解法而理解到，也順帶複習以前沒有學好的資料結構，搞懂什麼是 heap 啊。

上述演算法從 k lists 中，挑出最小資料元素的複雜度是 O(k)，但如果採用 heap 資料結構，確保每次可以拿到最小的資料 (min-heap)，若該 heap 只有 k 元素，每次插入新元素複雜度只要 O(k)，取得並移除最小值元素的複雜度也是為 O(k)。

Pop 操作示意圖

Push 操作示意圖

幸好，Go 標準函式庫中也有 heap 的實作，所以寫起來還算是輕鬆。

/**
* Definition for singly-linked list.
* type ListNode struct {
*    Val int
*    Next *ListNode
* }
*/

type PriorityQueue []*ListNode
func (pq PriorityQueue) Len() int {
   return len(pq)
}
func (pq PriorityQueue) Less(i, j int) bool {
   return pq[i].Val < pq[j].Val
}
func (pq PriorityQueue) Swap(i, j int) {
   // Swap, Go syntactic sugar
   pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
   item := x.(*ListNode)
   *pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {
   old := *pq
   n := len(old)
   item := old[n-1]
   *pq = old[0 : n-1]
   return item
}
func mergeKLists(lists []*ListNode) *ListNode {
   pq := make(PriorityQueue, 0, len(lists))
   for _, v := range lists {
      if v != nil {
         pq = append(pq, v)
      }
   }
   heap.Init(&pq)
   var head, itr *ListNode
   for pq.Len() > 0 {
      ele := heap.Pop(&pq).(*ListNode)
      if ele.Next != nil {
         heap.Push(&pq, ele.Next)
         ele.Next = nil
      }
      if itr == nil {
         head = ele
         itr = ele
      } else {
         itr.Next = ele
         itr = itr.Next
      }
   }
   return head
}

假設 k lists 中，共有 N 個資料元素，計算此演算法複雜度：