LeetCode #42 Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example,
Given [0,1,0,2,1,0,3,2,1,2,1], return 5.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

剛開始的分析與解法

初次見到這個題目，一時之間其實是沒有任何想法的，主要原因是對於題目的理解還不夠完全，對於什麼樣的情況會留住雨滴，還沒有辦法幻化成數字規則⋯⋯。

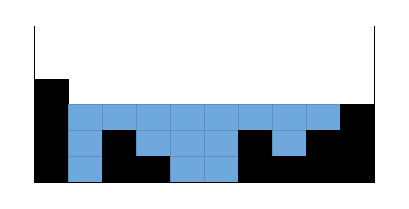
簡單的觀察是，如果海拔圖是能化成下面情況的話，左右最兩側的海拔高度最高：

那麼就可以計算要多少雨量被留著：

func min(m, n int) int {
   if m < n {
      return m
   }
   return n
}
func trap(height []int) (rain int) {
   if len(height) <= 2 {
      return 0
   }
   mh := min(height[0], height[len(height)-1])
   for i := 1; i < len(height)-1; i++ {
      rain += mh - height[i]
   }
   return
}

因此想法很簡單，給一組海拔圖，如果能把其拆成數塊滿足上述規則的海拔圖，然後把每塊海拔圖區塊的留住雨量，便能解決這個問題。

每次給予 height 海拔圖中，尋找地形中最高海拔高度，若其高度若大於左右兩側的高度，則由該高處位置拆成兩個海拔圖，然後再分別計算能留住雨量。否則套用先前提到的演算法計算留住雨量：

使用 Go Slice 的特性，加上遞迴計算便能寫出一段還算是優雅的程式碼：

func min(m, n int) int {
   if m < n {
      return m
    }
   return n
}

func trap(height []int) (rain int) {
   if len(height) <= 2 {
      return 0
   }

   // Find peak
   k := -1
   for i := 1; i < len(height)-1; i++ {
      if h := height[i]; k == -1 || h > height[k] {
         k = i
      }
   }

   mh := min(height[0], height[len(height)-1])
   if height[k] <= mh {
      // Calc.
      for i := 1; i < len(height)-1; i++ {
         rain += mh - height[i]
      }
   } else {
      // Split
      rain = trap(height[0:k+1]) + trap(height[k:])
   }
   return
}

若假設有 n 個海拔高度資料，那麼此演算法的空間複雜度為 O(1)，時間複雜度是 O(nlogn)。

受到啟發的分析與解法

現在每次解完題目都會刻意去看別人的解題思維，雖然經常會有自己很弱的挫敗感，但收穫也是滿滿。

計算任一點留住雨量的概念是，可以用以下例子解釋，預計算 A 點留住雨量 (高度為 height[A])，由該點往左邊看之最高點為 L (高度為 height[L])，往右邊看之最高點為 R (高度為 height[R])，因此可計算其留住雨量為 min(height[L], height[R]) - height[A]。

假設 lh(i) 計算 i 位置其左邊最高海拔高度，lh(i) = max(height[i], lh(i-1))，而且 lh(0) = height[0]。同理計算右邊最高海拔高度 rh(i) 同樣的概念，rh(i) = max(height[i], rh(i+1))，而且 rh(len(height)-1) = height[len(height)-1]。這樣的函數可以採用 Dynamic programming 方式來解，因此寫出以下更簡潔的程式碼：

func min(n, m int) int {
   if n < m {
     return n
   }
   return m
}

func max(n, m int) int {
   if n > m {
     return n
   }
   return m
}

func trap(height []int) int {
   if len(height) <= 2 {
      return 0
   }
   
   lh := make([]int, len(height))
   rh := make([]int, len(height))
   // Left peak
   lh[0] = height[0]
   for i := 1; i < len(height); i++ {
      lh[i] = max(lh[i-1], height[i])
   }
   
   // Right peak
   rh[len(height)-1] = height[len(height)-1]
   for i := len(height) -2; i >= 0; i-- {
      rh[i] = max(rh[i+1], height[i])
   }
   
   t := 0
   for i, h := range height {
      t += min(lh[i], rh[i]) - h
   }
   return t
}

若假設有 n 個海拔高度資料，那麼此演算法的空間複雜度為 O(n)，時間複雜度是 O(n)。