LeetCode #84 Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

For example, given heights = [2,1,5,6,2,3], return 10.

給予一直方圖 (histogram) 的資料，假設每條柱子 (bar) 寬度都為 1，計算其最大矩形 (rectangle) 面積，可參考其題目示意圖。

解法一：暴力法

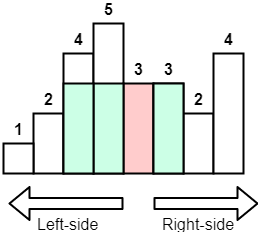
直覺的想法，針對直方圖的每一條柱子，計算其高度在鄰近柱子的矩形面積，然後比較回傳最大的矩行面積即可，其計算矩形面積也很容易，分別向左右邊柱子方面尋找，找到其柱子比當前柱子高度小就停止，之後計算其矩形面積，參考示意圖：

因此寫出以下解法，假設直方圖共有 n 的柱子，其演算法時間複雜度為 O(n²)，空間複雜度為 O(1)：

func largestRectangleArea(heights []int) int {
   maxArea := 0
   for i := 0; i < len(heights); i++{
      area := heights[i]
      
      // Left side
      for k := i-1; k >= 0; k--{
         if heights[k] >= heights[i]{
            area += heights[i]
         }else{
            break
         }
      }
      
      // Right side
      for k := i+1; k < len(heights); k++{
         if heights[k] >= heights[i]{
            area += heights[i]
         }else{
            break
         }
      }
      
      if area > maxArea{
         maxArea = area
      }
   }
   
   return maxArea
}

解法二：使用 Stack

解法一效率比較差，思考有沒有辦法只要跑一次直方圖 O(n) 就能夠計算完畢的演算法，經由推敲與關鍵字，使用 Stack 先進後出的特性，來計算每個柱子所佔據的矩形面積，然後最後回傳最大的矩形面積。

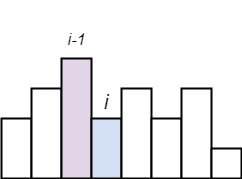
假設與之前一樣，由直方圖最左邊柱子掃描到最右邊的柱子，先考慮到兩種 Case，第一種是 i 柱子比 i-1 柱子還要高，那表示 i-1 柱子還可以繼續延展向右邊其矩形面積，且 i 柱子也可以開始計算其矩形面積，i 柱子為其矩形最右側的柱子：

反之第二種 Case，是 i 柱子比 i-1 柱子還要矮，那表示 i-1 柱子已經沒有辦法延展其矩形面積，可以計算該柱子的矩形面積，並且之後與最大矩形面積最比較，而 i 柱子一樣是開始計算其矩形面積，但該柱子將不會在是其矩形最右側的柱子：

首先先準備一個 stack 紀錄每個柱子的索引 (index)，每個未計算其矩形面積的柱子，都必須將其索引 push 到該 stack 中。若該柱子的高度比 stack 末端紀錄 (peek) 的柱子高度還要低的話，便執行第二種 Case 的處理。

將 stack pop 取得其柱子索引以取得該柱子高度，其矩形最右側柱子索引是 i-1，而最左側柱子索引則是看 stack 目前末端紀錄，會是為 stack.peek() + 1，因此其矩形寬度為 (i-1) - (stack.peek() + 1) + 1。

若 stack 已經沒有任何柱子索引資料，那表示會是下圖 i-1 柱的例子，其矩形最左側柱子索引為 0，其寬度會是 (i - 1) - (0) + 1：

有矩形高度與寬度便能計算其矩形面積，找到最大的矩形面積回傳即可，完成以下程式碼實作，假設直方圖共有 n 的柱子，其演算法時間複雜度為 O(n²)，空間複雜度為 O(n²)：

type stack []int

func (s stack) Peek() int {
   return s[len(s)-1]
}

func (s stack) Push(v int) stack {
   return append(s, v)
}

func (s stack) Pop() (stack, int) {
   l := len(s)
   return s[:l-1], s[l-1]
}

func (s stack) Len() int {
   return len(s)
}

func newStack(capacity int) stack {
   return stack(make([]int, 0, capacity))
}

func largestRectangleArea(heights []int) int {
   if heights == nil || len(heights) <= 0{
      return 0;
   }

   maxArea := 0
   stack := newStack(len(heights))
   heights = append(heights, 0)  // dummy end
   
   for i := 0; i < len(heights); i++ {
      ch := heights[i]
      for stack.Len() > 0 && ch <= heights[stack.Peek()] {
         h:= heights[stack.Peek()]
           stack, _ = stack.Pop()
         w := i
         if stack.Len() > 0{
            w = i -1 - stack.Peek()
         }

         if area := h * w; area > maxArea{
            maxArea = area
         }
      }
      
      stack = stack.Push(i)
   }
   
   return maxArea
}

這實作並不是一次到位，先是實作以下的程式碼，在 Leetcode 確定能通過所有測試後，才去尋找其他大神們的解法，最後從頭實作以上的程式碼。

這兩個程式碼在 Leetcode submissions 上顯示的執行時間都差不多，接近 20 ms，但是以上的程式碼相較之下非常簡潔許多，越比較真的是越沒自信呢。

type data struct {
   Height int
   Start  int
}

type stack []data

func (s stack) Peek() data {
   return s[len(s)-1]
}

func (s stack) Push(v data) stack {
   return append(s, v)
}

func (s stack) Pop() (stack, data) {
   l := len(s)
   return s[:l-1], s[l-1]
}

func (s stack) Len() int {
   return len(s)
}

func newStack(capacity int) stack {
   return stack(make([]data, 0, capacity))
}

func largestRectangleArea(heights []int) int {
   maxArea := 0
   stack := newStack(len(heights))
 Add  Dummy
   for i := 0; i <= len(heights); i++ {
      ch := 0
      start := i
      
      if i < len(heights) {
         ch = heights[i]
      }
      
      for stack.Len() > 0 {
         sd := stack.Peek()
         sh := sd.Height
         if ch < sh {
            if area := (i - sd.Start) * sh; area > maxArea {
               maxRectange = rectange
            }
            stack, _ = stack.Pop()
            start = sd.Start
         } else {
            break
         }
      }
      
      stack = stack.Push(data{
         ch,
         start,
      })
   }
   
   return maxRectange
}